Novel interpretation of the Delta-Epsilon Proof (maybe)

While writing my calculus blog, I found (perhaps even discovered) a new way of thinking about the $\delta$ – $\varepsilon$ (delta-epsilon) proof. This interpretation won’t cause any kind of epistemic revolution in mathematics, but I believe it’s a helpful pedagogical tool worthy of its own blog post.

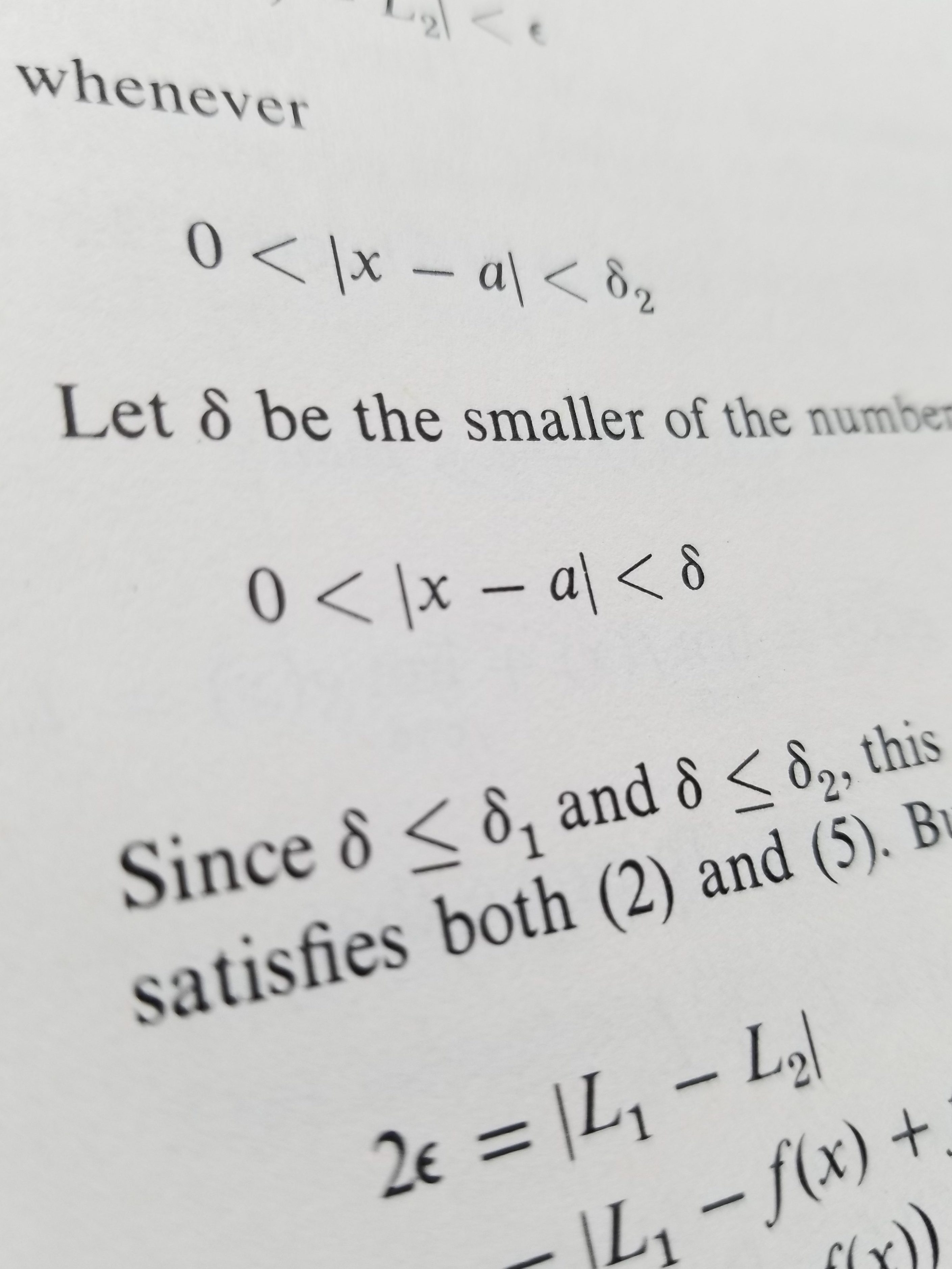
In case you have forgotten, the limit definition states the following (where $a$ and $L$ are real numbers):

Let $f(x)$ be defined for all $x$ in some open interval containing the number $a$ , with the possible exception that $f(x)$ may or may not be defined at $a$ . We will write

$\lim_{x \to a} f(x) = L$

if given any number $\varepsilon > 0$ , we can find a number $\delta > 0$ such that $f(x)$ satisfies

$|f(x) - L| < \varepsilon$ whenever $x$ satisfies $0 < |x - a| < \delta$

To prove a limit statement, we have to show that the limit satisfies this definition. How do we do this? We assume $\varepsilon$ exists and show that, no matter what the value of $\varepsilon$ is, there exists a corresponding $\delta$ . The mechanical procedure is as follows: Reduce the $f(x)$ condition down to the $x$ condition, find the restriction on the $x$ condition, and equate that restriction to $\delta$ .

Taking a simple example:

Prove $\lim_{x \to 2} (3x - 5) = 1$

Soln. We must show that given any positive number $\varepsilon$ , we can find a positive number $\delta$ such that $f(x) = 3x - 5$ satisfies

$|(3x - 5) - 1| < \varepsilon$ (i)

whenever $x$ satisfies

$0 < |x - 2| < \delta$ (ii)

To find $\delta$ , we must manipulate the $f(x)$ condition until it looks like the $x$ condition. We can rewrite (i) as

$|3x - 6| = 3|x - 2| < \varepsilon$

$|x - 2| < \frac{\varepsilon}{3}$ (iii)

We have now reduced (i) to look like (ii). Earlier, we stated that $|x - 2|$ is less than $\delta$ , but now we see that it’s less than $\frac{\varepsilon}{3}$ . We thus deduce that

$\delta = \frac{\varepsilon}{3}$

We have just shown that for a given $\varepsilon$ satisfying (i), there exists a $\delta$ satisfying (ii). In other words, the conditions of the limit definition are satisfied and the limit is true.

Q.E.D.

One of the things I always wondered when doing such computations was “How can we be certain that the $x$ condition’s boundary was the greatest boundary possible.” That is, how do we know that there isn’t a bigger boundary that still satisfies the conditions.

Well, after a lot of intellectual struggle and Socratic rumination, I came up with a different way of thinking about the reduction of the $f(x)$ condition that makes it obvious how this is certain.

Consider the following:

Imagine a function $g$ that takes as its input the distance between $x$ and $a$ (i.e. $|x - a|$ ) and outputs the distance between $f(x)$ and $L$ (i.e. $|f(x) - L|$ ).

In this view, the restriction on the $f(x)$ condition is really just a restriction on $g(x)$ .

From middle school algebra, we know that we can apply a restriction on the output of a function and then reduce that output to the input. When we do this, we get a corresponding restriction on the input. This restriction is such that, when satisfied, the output restriction is satisfied. For example, let

$f(x) = 3x$ :

Stipulating $f(x) < 6$ , we can find the input restriction that leads to this being true. We do that by reducing $f(x)$ to the input $x$ :

$3x < 6$

Dividing by 3, we obtain

$x < 2$

This is the input restriction that satisfies the output restriction. Notice that any $x$ value above 2 leads to an output that is greater than 6.

Thus, reducing $g(x)$ with the $\varepsilon$ restriction will produce the input with its $\delta$ restriction, a restriction which is the greatest possible. Since $g(x)$ is simply the distance between $f(x)$ and $L$ , we are truly finding the upper bound that the distance between $x$ and $a$ must stay below in order for the $f(x)$ condition to be satisfied.

Interpreting $\delta$ – $\varepsilon$ proofs this way, makes our actions quite reasonable.

Share this:

Related