This is a short post where I briefly describe cross products and dot products. If you have not previously studied linear algebra, the math may be a tad complicated.
Cross products
The cross product of two 3D vectors u and v () defines the components of the vector that is orthogonal (perpendicular) to both. That is all! Quite simple. The formula is similarly intelligible.

For vectors and
, their cross product would be
A better way of writing this would be in terms of determinants as so
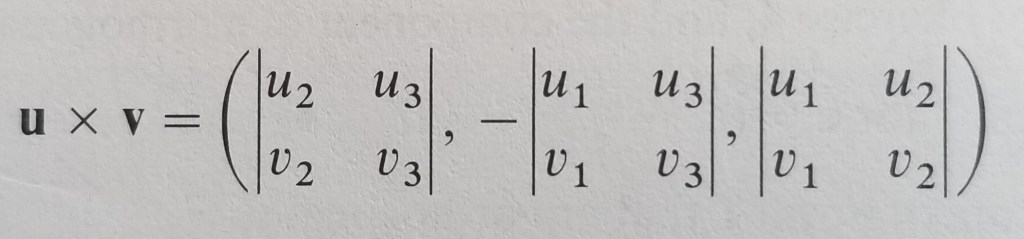
This formula can be remembered by considering the 2×3 matrix

whose first row is constituted of the components of u (the first factor) and whose second row is constituted of the components of v (the second factor). The determinant in the first component of is obtained by taking the determinant of the submatrix that results when we delete the first column. The determinant in the second component is obtained by deleting the second column and prepending a negative sign. The determinant in the third component is obtained by deleting the third column.
When we do this operation, we will obtain the components of a vector that is orthogonal to both u and v.
Dot products
The dot product of two vectors u and v is defined as
(Those absolute values are supposed to be the symbols for the norm of a vector. The LaTex I’m using doesn’t support the standard symbols).
This may also be written as
and can be described in words as the sum of the products of the corresponding components. I encourage the reader to look up the method we use to obtain this simpler version.
While I haven’t gotten far enough in my linear algebra book to understand the utility of the dot product, I do know that it can be used to find the angles between two vectors as follows:
- Use
to find the value of the dot product.
- Plug this value into
.
- Solve for theta.
I recommend trying to find the angle between the body diagonal of a cube and one of its edges. It’s a fun challenge.
Differences
The main reason behind me writing this blog is to allow me to remember the difference between these two ideas:
Despite their names sounding similar, the dot product defines a scalar, while the cross product defines a vector.
