Orthogonal projections in linear algebra

In linear algebra, we are occasionally interested in resolving vectors into their “projections.” In contrast with components, however, which are determined with respect to the x- and y-axis, projections are determined with respect to an adjacent vector, one that shares the same initial point.

This blog discusses the derivation of formulas that help us in finding these projections.

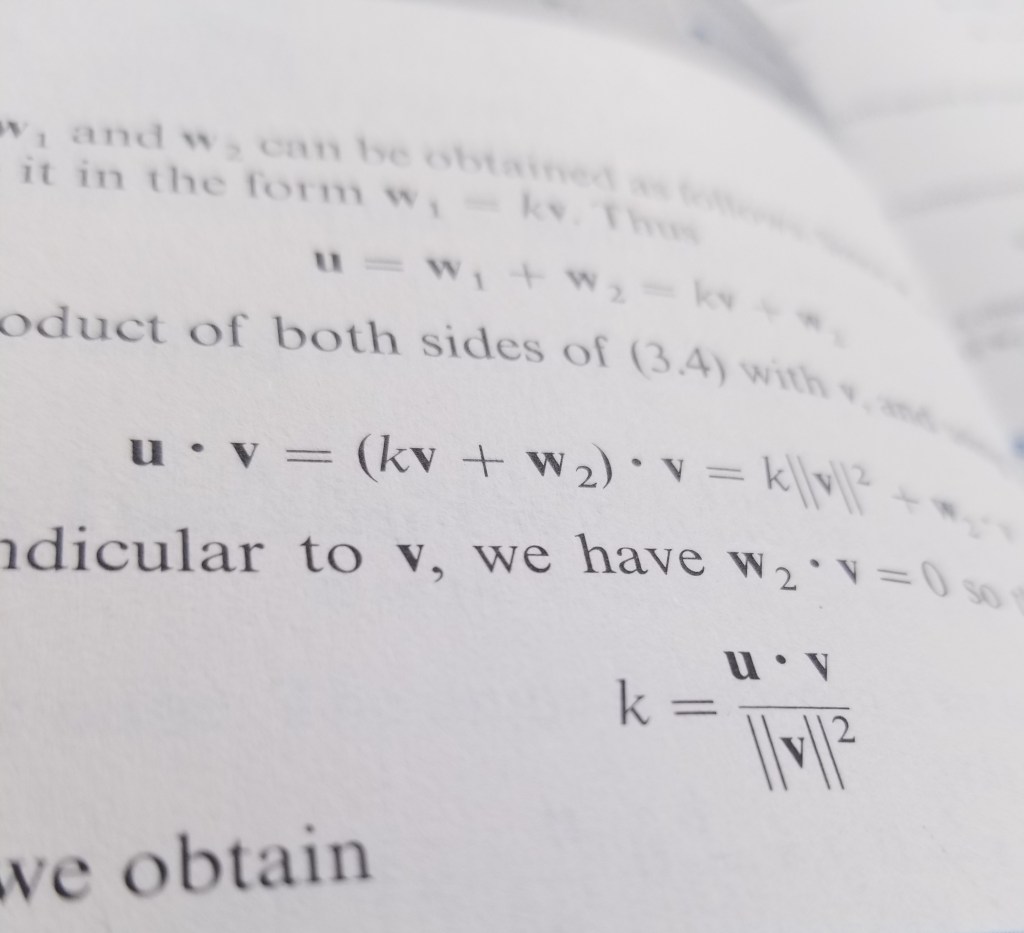
Suppose we have two nonzero vectors u and v in 2-space. The vector u can be written as a sum of vectors, say, $\mathbf{w}_1$ and $\mathbf{w}_2$ :

$\mathbf{u} = \mathbf{w}_1 + \mathbf{w}_2$ (i)

where $\mathbf{w}_1$ is constructed to be parallel to the adjacent vector v and $\mathbf{w}_2$ is made to be orthogonal (perpendicular) to it, as shown below.

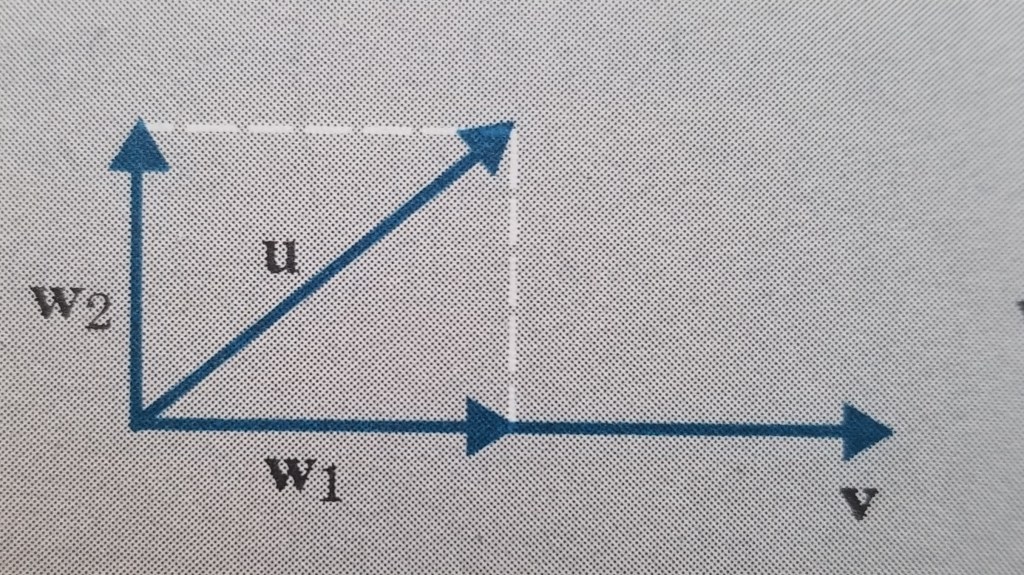
In the diagram, vector $\mathbf{w}_1$ is called the orthogonal projection of u on v and vector $\mathbf{w}_2$ is called the component of u orthogonal to v.

Since $\mathbf{w}_1$ is simply a scaled version of vector v, it can be written as

$\mathbf{w}_1 = k\mathbf{v}$ (ii)

where k is a scalar.

The formulas we are in pursuit of are those that express $\mathbf{w}_1$ and $\mathbf{w}_2$ in terms of just u and v. With this in mind, let us substitute (ii) into (i):

$\mathbf{u} = k\mathbf{v} + \mathbf{w}_2$ (iii)

To get rid of $\mathbf{w}_2$ , take the dot product of each side with v.

$\mathbf{u} \cdot \mathbf{v} = (k\mathbf{v} + \mathbf{w}_2)\cdot \mathbf{v}$

$\mathbf{u}\cdot\mathbf{v} = k(\mathbf{v}\cdot\mathbf{v}) + \mathbf{w}_2\cdot\mathbf{v}$

Notice that $\mathbf{w}_2$ and v are orthogonal vectors. Thus, their dot product is zero. The dot product $\mathbf{v}\cdot\mathbf{v}$ is equal to $||\mathbf{v}||^2$ .

$\mathbf{u}\cdot\mathbf{v} = k||\mathbf{v}||^2$

Solving for k,

$k = \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{v}||^2}$

Good. Now we have the scalar k in terms of just u and v. From here, we simply substitute k into (ii):

$\mathbf{w}_1 = \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{v}||^2}\mathbf{v}$

We have successfully derived the formula for the orthogonal projection of u on v. Now, we can substitute this into our vector sum from earlier ( $\mathbf{u} = \mathbf{w}_1 + \mathbf{w}_2$ ).

$\mathbf{u} = \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{v}||^2}\mathbf{v} + \mathbf{w}_2$

Solve for $\mathbf{w}_2$ .

$\mathbf{w}_2 = \mathbf{u} - \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{v}||^2}\mathbf{v}$ .

Done! We have just derived general formulas for the projections of u with respect to an adjacent vector v. All that is necessary from the user’s end is to plug in the components of each vector, solve a couple of dot products, and recall how to calculate the norms of vectors.

A wonderful derivation, indeed!

Share this:

Related